kort handledning av Astro.xls
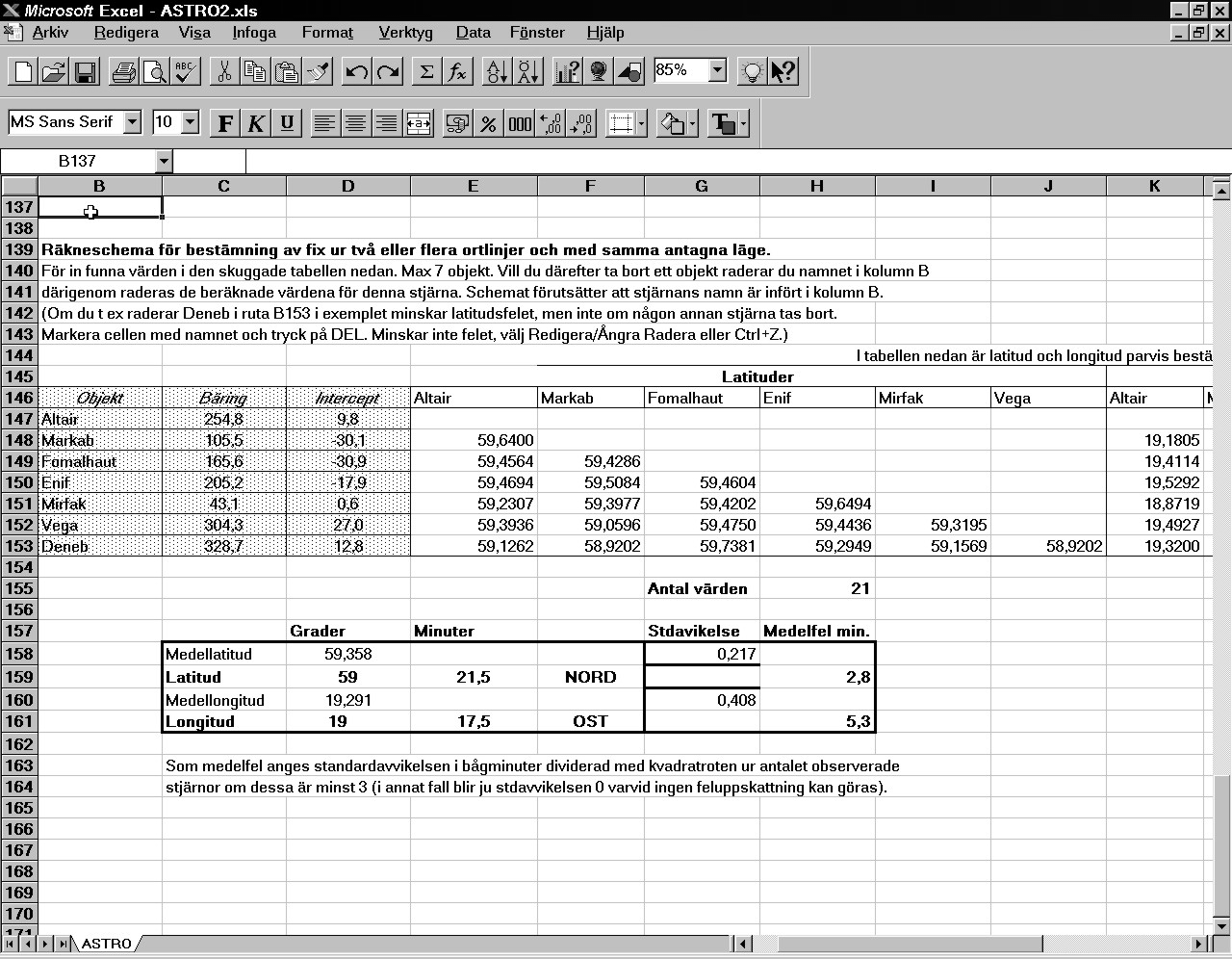
| ASTRO.XLS av Carl Erik Tovås Kortfattad handledning Beräkningsschemat är i form av ett kalkylblad i Excel, men kan förstås laddas in även av andra kalkylprogram (med reservation för ev. "egenheter"). Beräkningarna utgår från år 2000 och kan backas eller föras fram ungefär 100 år utan att noggrannheten nämnvärt ändras. Höjdberäkning basat på funnen sextantshöjd och räknat läge. Med schemat kan man beräkna sann höjd och azimuth till solen och de 57 navigationsstjärnorna. Man får också det s k interceptet, dvs avståndet i sjömil mellan antagen position och den ortlinje som går vinkelrätt mot azimuthen. Man ska mata in följande värden: · I rad 8 matar in datum, GMT, objekt. Det senare är namnet på stjärnan (rätt stavat) eller "solen" vid solhöjd. · I rad 18 matar man in beräknad lat och long samt observerad sextantshöjd utan korrigering. · Vid solobservation måste man även mata in värdet -1 eller 1 i cell F18 för observerad soldel (-1 för nedre kant, 1 för övre). · I rad 22 slutligen matar man in sextantsfelet med ombytt tecken (rättelsen!), ögats höjd, lufttrycket och temperaturen. Inmatningen av grader, minuter och delar av minuter sker i formen (D)DD,MMd, dvs först hela grader, sen decimalkomma följt av två siffror för minuterna och sist en decimal. Vid västlig longitud och sydlig latitud ska ett minustecken föregå graderna. Programmet beräknar därefter automatiskt lokal tid, azimuten och interceptet efter att först ha omräknat minuter (och tidssekunder) till decimal form. Resultatet syns bl a i cellerna H10och I 10 men repeteras också i cellerna B-C 27 för solen och i kolumn K och L för aktuell stjärna vid stjärnobservation. I rad 27 och 28 ges ytterligare information i form av beräkningar av solens deklination, apparent höjd, räknad dvs sann höjd samt GHA för vårdagsjämningspunkten både i grader och minuter och i decimalform. I cellerna G30-31 ges apparenta solhöjden med korrektion för observerad limb och atmosfäriska förhållanden. Raderna 34-56 är dolda. Denna del innehåller detaljer i beräkningarna och kan förstås göras tillgänglig genom att öka radhöjden från 0. Samtliga celler för beräkningar som innehåller formler är låsta för att ingen olycka ska ske. De kan låsas upp med kodordet JAG, men jag varnar för detta eftersom det är lätt att förstöra schemat. Preliminär bestämning av lämpliga stjärnor för observation Genom att mata in räknat läge vid en tidpunkt i närheten av skymning eller gryning kan man (utan att behöva mata in sextantsvärdena) få uppgift om bäringen till de 57 stjärnorna samt deras höjd över horisonten. Resultatet visas i området F80-I136 där också stjärnans namn samt magnitud finns angivna. Man väljer sen ut ett antal av dessa stjärnor för observation när tiden är inne. Man bör välja minst 3 och högst 7 med lämplig höjd (15-75°) och spridda bäringar. Välj de starkaste stjärnorna (minsta värdet på magnituden) och undvik stjärnor med kontrabäring. Stjärnobservationer för bestämning av position Genom att ställa in sextanten på funnen höjd och sikta i bäringen hittar man lätt resp. stjärna och kan mäta höjden. Anteckna exakta tidpunkten och värdet och mät mot nästa stjärna osv. På detta sätt fås en uppsättning höjder tagna vid samma eller närliggande tidpunkt. Mata in exakt tid för observationen (D8-F8), stjärnans namn (G8) samt funnen sextantshöjd (G18) (Vid behov även nya värden -- men bara en gång -- i B18 och D18 samt B22-E22.) Läs av azimuten (bäringen) och interceptet i cellerna H8-I8 samt för in dessa värden och stjärnans namn i tabellen B146-D153. När samtliga observationer behandlats på detta sätt får man en tabell med positioner i form av latitud och longitud beräknad för varje par observationer. Har man gjort minst 3 beräknas även standardavvikelsen och standardfelet i positionen. Skulle resultatet av någon observation märkbart avvika från de övriga kan man radera denna stjärnas namn i kolumn B och observera om medelfelet minskar (minst 4 observationer krävs i så fall innan man raderar, eftersom bara 2 observationer med automatik ger standardavvikelsen 0). Screenshot av ett tänkt resultat
Lycka till! |